DISCLAIMER: This web page is a simply a mirror of http://sleepingsquirrel.org/monads/monads.html, which appears to have disappeared from the Internet entirely. I do not claim ownership of the following content, if you are the author and you wish for this page to be removed, please email weitzeug [at] gmail [dot] com.
Monads in Perl
(in the spirit of TMTOWTDI)
Haskell is the language that popularized (?!) monads, but my
understanding was impeded because of the myriad of new things that I
needed to learn about Haskell before I could even get to monads
(different syntax, purity/laziness, typing system, significant
white-space, etc.) All that added up to something as clear as mud. I
needed a Rosetta Stone to help me decipher this new language and its
features. I decided I should transliterate a few monad programs
into a language I could better understand. And I choose perl. Once I
did that, then things became *much* clearer to my imperative brain.
This article isn't intended to give a complete explanation of what
monads are. It is a supplement to be used along with the many other
monad tutorials out there. Here's hoping that this is as much a help to
you as it was for me.
Monads are one method programmers in pure functional languages use
to simulate side-effects (like state and I/O) which aren't normally
allowed by their language. Perl doesn't have many limitations when it
comes to side-effects (like variable assignment, printing, etc. (But
don't press your luck by doing too much in a signal handler)). There
are numerous tutorials on the 'Net, but a lot of them seem to assume a
high-level mathematics background and none have used Perl as their
implementation language. So let's remedy that. Monads do two separate
things for us. They simulate state (allowing things like assignment
[a=a+1]) and they provide an ordering to our functions (to make sure
things like I/O get executed in the correct sequence).
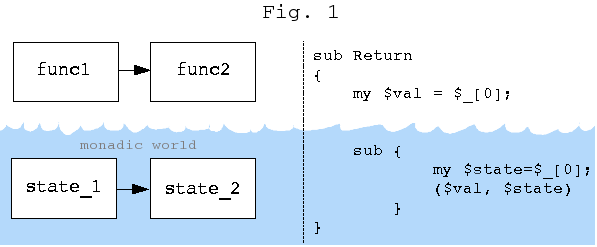 If you squint a little bit and try not to carry the idea too far,
you can think of monads as sort-of-kind-of like tied functions (if Perl
actually had such a beast). When you would try to compute something
with one of these tied functions (i.e. by calling it), perl would also
invoke some hidden procedure which acts upon our state. (Fig. 1)
If you squint a little bit and try not to carry the idea too far,
you can think of monads as sort-of-kind-of like tied functions (if Perl
actually had such a beast). When you would try to compute something
with one of these tied functions (i.e. by calling it), perl would also
invoke some hidden procedure which acts upon our state. (Fig. 1)
Sequencing
In Haskell, you don't specify the order of execution, but
that doesn't mean that there isn't one. All data dependencies need to
be met. Think of a system of simultaneous equations...
X = 1 + 1
Y = 2 * 3
Z = X + Y
Both X and Y have to be computed before Z can be evaluated. You can
think of lazy functions being like file handles or sockets that block until
their answer is known. Pretend that all functions X,Y and Z are
executing parallel, but Z is blocked until both X and Y are available.
#use forking open to start 3 more processes
unless (open X, "-|") {sleep(5); print 1+1; exit }; # X=1+1
unless (open Y, "-|") { print 2*3; exit }; # Y=2*3
unless (open Z, "-|") { print <X>+<Y>; exit }; # Z=X+Y
print "Z=\n";
print <Z>."\n";
In this example, since X and Y don't have side effects, evaluating X
first vs. Y first doesn't matter. But if X had the side effect of
opening a file and Y was closing a file, you'd better make sure it gets
executed in the proper order. Below is the canonical example of a set
of functions that have a data dependency.
#data dependency and manually passing state around
#count how many times some_func gets called
$state0 = 0; #initial state
($a,$state1) = some_func($x, $state0);
($b,$state2) = some_func($y, $state1);
($c,$state3) = some_func($z, $state2);
sub some_func
{
my $state = $_[1];
blah; blah;
return (blah, $state+1);
}
And here is how you would normally do it with global variables in a
strict language...
#Mutable state -- global variable
our $state = 0;
$a = some_func($x);
$b = some_func($y);
$c = some_func($z);
sub some_func
{
blah; blah;
$state++;
return blah;
}
We know that our functions will be executed in the proper order if
thy depend on one another, but
what do we do if our functions don't naturally depend on one another? We
make a dependency up out of thin air.
#Create artificial dependency
#assume some_func1 and some_func2 don't normally take arguments
$world2 = some_func1($world1);
$world3 = some_func2($world2);
Hmmmm... Making up useless variables doesn't sound very scientific, but
don't worry, they get optimized away.
The first pass of the compiler will analyze the dependencies and make
sure the operations get executed in the proper sequence. Then the optimizing pass
will eliminate the spurious "$world" we've invented. Once we've got an
execution order defined, we can execute side-effecting code all we like.
Well, almost. Haskell is supposed to be referentially
transparent, but what about functions like getCh? Obviously they
can't be referentially transparent, right? That is correct. So Haskell
provides a language primitive to deal with this. It is known as
"ccall", and it takes a pointer to a C function, calls it, and returns
its result. "ccall" is defined to be strict (non-lazy) and it is also
flagged as being not referentially transparent, so the compiler won't
perform optimizations which depend on that property.
Once we've identified a need to create dependencies, we can start to
recognize patterns in our code and build functions to abstract them
away.
# "Then" factors out commonalities in the above code
$s = Then(&some_func1, Then(&some_func2, &some_func3));
sub Then
{
($f, $more) = @_;
return sub{
my $world1 = shift;
my $world2 = $f->($world1);
my $world3 = $more->($world2);
}
}
Data
Essentially a monad is a hidden data structure (Fig. 1) which
automatically passes state around for us. We could manually pass state
into functions and pass it back out again like we've seen, but this is tedious
and boring. Monads supposed to be a way of letting the machines do the work for
us.
These hidden data structures are composed of closures (also know as
anonymous subroutines). Before we get too involved, let's see just what
sorts of data structures we can build with closures. Below is a list
made of closures.
$l = sub{(3.14, sub{(2.7, sub{(1, sub{(0,undef)})})})};
When $l is executed, it returns a pair, the first item of the pair
is the next value in the list (the head), and the second item is a closure
which represents the rest of the list (the tail). We can create functions
which manipulate this new type of list we've just created.
sub head #returns the head of a list
{
(my $h, my $t)=$_[0]->() if defined($_[0]);
return $h;
}
sub tail #returns tail of a list
{
(my $h, my $t)=$_[0]->() if defined($_[0]);
return $t;
}
sub cons #helper function to construct new lists
{
my $val=shift; my $list=shift;
return sub { return ($val, $list) }
}
With the new cons() function we could create our original
list like cons(3.14, cons(2.7, cons(1, cons(0,undef))))
And here's a version of map (notice the capital 'M')...
sub Map
{
my $f=shift; my $list=shift;
(my $head, my $tail)=$list->() if defined($list);
defined($tail) ? sub{ ($f->($head),Map($f,$tail)) }
: sub{ ($f->($head),undef) };
}
This is how you'd invoke it $f=Map(sub{2*$_[0]+1},$g); .
We can also do infinite lists...
sub zeros #endless supply of 0's
{
return sub{ (0,zeros()) }
}
...and we can combine all this stuff...
$x=cons(3, zeros()); #a three and lots of zeros
$y=Map(sub{$_[0]+2}, $x); #add two to everything
So that is a demonstration that closures can be use to store data,
but how does that fit into the scheme of things? Closures are the
closest thing we have to state in a pure language. In mathematical
terms, you can think of it as taking an equation and binding one of its
free variables to a particular value.
Currying & Lambda Abstraction
In order to provide a more direct translation of Haskell code into
perl we need to discuss currying. In perl, we have to perform currying
by hand. Here's an example of a function which takes one curried value.
sub add { $_[0] + $_[1] };
sub curried_add
{
$arg1 = $_[0];
return sub { add($arg1, $_[0]) };
}
$plus5 = curried_add(5);
print $plus5->(6); # eleven
print curried_add(3)->(4); # seven
Lambda abstraction (creating anonymous subroutines) is also more verbose
in perl. Here's an example of an anonymous function that increments its
argument by one.
--Haskell
y = \x -> x+1
#perl
$y = sub { my $x=$_[0]; return $x+1 }
Monads
Now we're getting down to the nitty-gritty. The code below comes from two
excellent paper on monads by Phil Wadler. The first is
Monads for functional programming and Imperative functional programming. Dr. Wadler has
also written a slew of other monad papers.
Here's the simple evaluator from _Monads For Functional Programming_.
It takes a string and performs divisions ("Div") of constant integers,
("Con 4"). The string "Div Con 18 Con 2" evaluates to 9, and Div Div
Con 18 Con2 Con 3" evaluates to 3.
#!/usr/bin/perl -w
my $question="Div Con 18 Con 2";
my $ans=ev($question);
print "ans=$ans\n";
sub ev
{
my $term = $_[0];
my $con=qr{Con (\d+)};
my $div; $div=qr{Div ($con|(??{$div})) ($con|(??{$div}))};
if($term =~ /^$con/)
{
return $1;
}
elsif($term=~/^$div/)
{
my $numer=$1; my $denom=$3;
return ( ev($numer)/ev($denom) );
}else{ print "Syntax error\n"; }
}
Now let's see if we can count the number of divisions performed in a
monadic way. Here's some Haskell pseudo-code to demonstrate the
functionality. (rename ">>=" and "return" to avoid name collision under Hugs and
GHC)
main = do
print (show (eval question 0)) -- the zero is the initial state
data Term = Con Int | Div Term Term deriving Show
question=Div(Div (Con 18) (Con 2)) (Con 3)
type M a = State -> (a,State)
type State = Int
return :: a -> M a
return a = \state -> (a,state)
(>>=) :: M a -> (a->M b) -> M b
func1 >>= func2 = \initial_state -> let (a,next_state) = func1 initial_state
(b,final_state) = func2 a next_state
in (b,final_state)
tick :: M ()
tick = \x -> ((),x+1)
eval :: Term -> M Int
eval (Con a) = return a
eval (Div t u) = eval(t) >>= \a -> eval(u) >>= \b -> tick >>= \y -> return(a `div` b)
Quick typing digression
In the above code, M the type of a stateful monad. More specifically, a function
of type M a is one that takes a State and returns a
(value, state) pair. When it gets boiled down, to basic terms, the type
of ">>=" (pronounced "bind") ends up
being pretty messy. Bind takes a function that takes a value and returns
a (value, state) pair as an argument. Bind returns a function (that
takes a function that takes a value and returns a (value, state) pair)
that returns a function which takes a value and returns a (value, state)
pair. Whew! That's why talking about monads in the abstract makes life
easier. We can instead say that bind (in its non-curried
implementation) takes two parameters: A.) a monadic value and B.) a
function for turning monadic values into other monadic values. Bind
then returns the monadic value resulting from applying B.) to A.). You can gloss
over these details just like you can ignore electromagnetic field theory
when explaing email to someone.
Monads in perl (finally...)
In perl we can't have subroutines with names like ">>=" and "return" so
we'll call them "Bind" and "Return" (note capital "B" & "R"). We
also don't have user definable infix operators, so this is going to be
at least a little bit ugly.
(code)
#!/usr/bin/perl -w
use strict;
use re 'eval';
my $question="Div Con 18 Con 2";
my @ans=ev($question)->(0); #pass in the curried initial state
print "Answer=$ans[0], Number of divisions=$ans[1]\n";
sub ev
{
my $term = $_[0];
my $con = qr{Con (\d+)};
my $div; $div = qr{Div ($con|(??{$div})) ($con|(??{$div}))};
if($term =~ /^$con/)
{
return Return($1);
}
elsif($term =~ /^$div/)
{
my $numer = $1; my $denom = $3;
return Bind(ev($numer))->(
sub{ my $n=$_[0];
Bind(ev($denom))->(
sub{ my $d=$_[0];
Bind(tick())->(
sub{ my $e=$_[0];
Return($n/$d)
})
})
})
}else{ die "Syntax Error: $term"; }
}
sub Return
{
my $val = $_[0];
sub {
my $state = $_[0];
($val, $state)
}
}
sub Bind
{
my $func1 = $_[0];
sub {
my $func2 = $_[0];
sub {
my $initial_state=$_[0];
(my $a, my $next_state) = $func1->($initial_state);
(my $b, my $final_state)=($func2->($a))->($next_state);
($b, $final_state)
}
}
}
sub tick { sub{ (undef,$_[0]+1) } }
Okay, that's probably something only a mother could love. Here's a
little source-filter module which provides a limited form of
Haskell's "do notion". We can clean up the "ev" subroutine to look
something like (full code)...
sub ev
{
my $term = $_[0];
if($term =~ /^$con/)
{
return Return($1);
}
elsif($term=~/^$div/)
{
my $numer=$1; my $denom=$3;
return DO {
my $n <- ev($numer);
my $d <- ev($denom);
my $g <- tick();
Return( $n / $d );
}
}else{die "Syntax Error: $term";}
}
Ah. Much nicer. Perl 6 is supposed to have currying, user defined
infix operators and host of other niceties which could make monads in
cleaner in that language.
Conclusion
Again, I heartily recommend reading Phil Wadler's monad papers and
translating his other examples into perl to really get a handle on
monads. Hopefully you are now on the road to further monad enlightenment.
Copyright © 2004 Greg Buchholz 
Last update: 24Aug2004
 If you squint a little bit and try not to carry the idea too far,
you can think of monads as sort-of-kind-of like tied functions (if Perl
actually had such a beast). When you would try to compute something
with one of these tied functions (i.e. by calling it), perl would also
invoke some hidden procedure which acts upon our state. (Fig. 1)
If you squint a little bit and try not to carry the idea too far,
you can think of monads as sort-of-kind-of like tied functions (if Perl
actually had such a beast). When you would try to compute something
with one of these tied functions (i.e. by calling it), perl would also
invoke some hidden procedure which acts upon our state. (Fig. 1)