
As this writing is a collection of my ideas that have not been written down before now, this page will be gradually updated and refined whenever I recall more and more of my ideas concerning the topic and feel the want. I will perhaps add more such pleasing patterns, eventually.
I introduce here what I refer to as Pleasing Patterns; I have no better name for these and quite like it by now. It is not uncommon to see a mobile phone with a three by three password mechanism in use. It was 2007 or 2008 when I first saw one of these in use and decided to create my own patterns, including that which I hold most dear. The base of these ideas is clearly not my own, as I did not create this password mechanism, but I have created some pieces I consider beautiful and have also created a format for storing such patterns, which is what is being introduced.
The following is the basic grid for these patterns:

The following is the true grid these images adhere to:

It is clear that the basic form of the grid can be summed in twenty bits, corresponding to each individual line segment being present or not. The true form of the grid merely increases this to thirty six bits. In my original envisioning, this was sufficient. However, I came to value the order of the pattern as being particularly important, enough so to warrant a format that preserved this. This also had the side-effect of forcing the patterns to be contiguous, which is a nice quality to have.
The numerical format for describing these patterns will now be described. Firstly, it is important that there be a mechanism for versioning and whatnot and so the first six bits are to be used for this, with this format being described having all set to zero. Following this will be the number of lines in the pattern, with six bits being sufficient. I do not consider it important to permit an empty such pattern and so the count can be thought of as being incremented, allowing one to sixty four lines. Following that is the starting point of the pattern, which requires four bits, and is described by the first bit indicating the ninth position if set to one and with the following three bits indicating the position otherwise. After this, the format is merely collections of three bits representing the following position from the previous. The following shows the positions of the grid, starting from one rather than zero, as that is more pleasant:

The following positions are ordered in a simple manner: the current position is merely skipped in the counting. Here is the ordering from the center position, the fifth position:

For some history of the format, I prefer to avoid leaving anything that could be considered a hole in my numerical formats and so had a different idea for specifying the starting position. The following depicts one ordering of the grid; another potential ordering has the third and fourth quadrants swapped for a clockwise ordering:

My original thinking was to split the four bit starting position code into two bit segments, with which the first half indicates the quadrant and the second half indicates the position within that quadrant. Expanding this to a table revealed the folly, as the center in particular was able to be specified in four ways whereas many positions had only a single unique specification.
An implementation and other tooling for this format is not yet in a state suitable for the public.
I will now display my pieces. The first is the oldest and is a simple alteration of a basic decimal two:

This is among the first I made and also the most precious to me. I started with a pattern from the center, went up and to the right, and I recall the rest flowing from my hand in such a pleasing way:

This was by far the most recent pattern, for a time, but still has a charm to it:

This pattern is also old, but the original was lost, I believe in the fourth quadrant according to the earlier ordering shown, and this is my closest approximation to it:
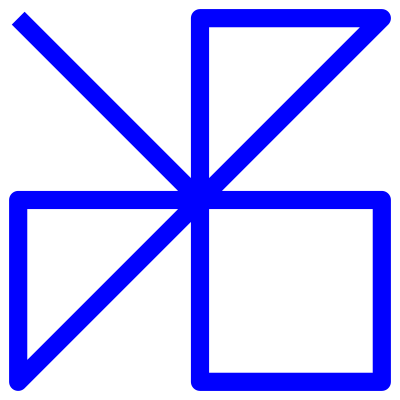
I've recently made some more patterns I quite enjoy. In errant thought, I was mulling over base thirty and how pleasant it is; thirty is the product of the first three primes, two, three, and five; sixty is a nice base, but humans seem to cope better with around thirty symbols, looking at some alphabets, so thirty seems a better base for this, but sixty is nice for time, although having a second two does make it less beautiful than thirty in some ways.
I considered the typical two-by-three format for displaying the decimal numbers and realized there was no reason you couldn't use this three-by-three format instead, and so started dedicating some patterns to these. I used a rather rigid design for these, as that's common with the former.
I also created some alternate designs for the decimal numbers, since I created some such symbols for those numbers ten and larger.
I took little issue with the common symbol for zero; it should clearly be blank if possible, but a suitable and explicit representation will likely be somewhat opaque.

The now common symbol for one is more stylized than is strictly necessary. The obvious such symbol is a single line, be it horizontal or vertical, but that is so simple I won't provide one here for now.

The now common symbol for two is awful, I think. It is composed of far more than two lines and does nothing to evoke the image of such an important number. My alternate two is rather pleasant, I think, as the lines must be connected and an acute angle shape doesn't seem to do it justice.

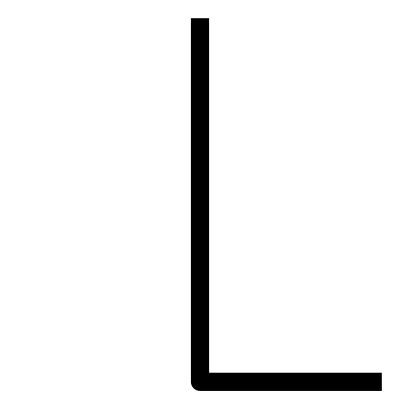
The now common symbol for three is not so bad as two, but is still more complex than necessary, although it does have three distinct features. It's a nice property, for at least the first few symbols to have lines equal to their magnitude, and I also enjoy making the prime symbols more distinct than those for the composite, and so I've also created an alternate three that I find nice; the original resembled a lightning bolt, imagine, but it also resembled my symbol for eleven and, rather than rotate this, I went with another solution I'd mulled over.


I have fewer remarks concerning the now common symbol for four. It could be made to resemble two more by adding a prong from the right tip that would resemble the initial flow of the two. My alternate four resembles my alternate two and contains four lines; it's obvious that this could be made to resemble the common symbol for four by transferring a single line, but that's much less pleasant, although it's good to keep in mind.
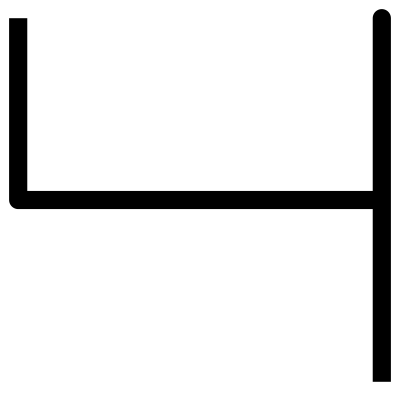

The common symbol for five is actually reasonably suitable. It contains five lines and is suitably distinct if one has an alternate two. Thus, I've no alternate symbol for five.

The common symbol for six loosely resembles the symbol for five. It could trivially be made to have six lines by either adding a bend in the beginning or a cross in the enclosed area, but both of these are insufficient. I currently have no alternate six symbol.

The common symbol for seven would be better suited to two. Seven lines is pushing the boundary of reasonable for a symbol, however. I currently have no alternate seven symbol, although I do have a stylized such symbol.


The common symbol for eight is also a poor such symbol. The two-by-three system also makes eight seem more significant than it truly is. My alternate eight symbol is derived from the four symbol and can be thought of as being composed of three of the two symbols, which is good, as eight is two to the third power. Further, drawing this alternate symbol by hand would even closely resemble the motions of drawing the common symbol.

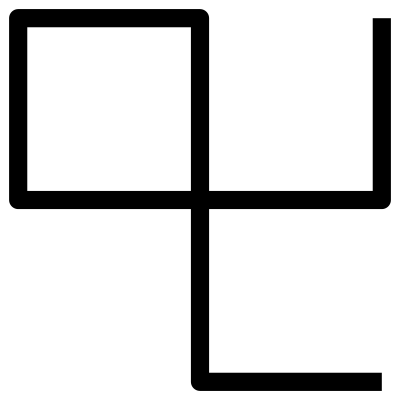
The common symbol for nine is also poor and resembles the common symbol for eight. My alternate nine appears to be composed of two of my alternate three symbols.


Now I move on to entirely new symbols. My symbol for ten is built from a five and my alternate two. There was another that was considered, but it didn't appear nearly so nice.
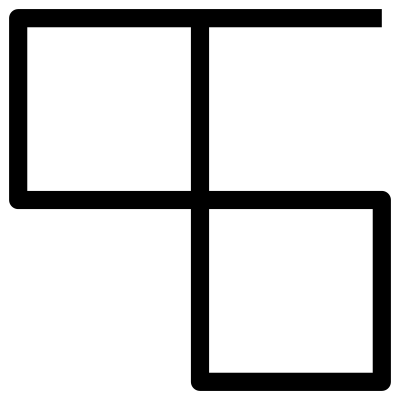
My symbol for eleven is meant to show eleven's unique status as a prime number and so resembles no others.

My symbol for thirteen was originally a stylized nine, but didn't work well for that purpose, but perhaps works well for thirteen, in its uniqueness and lack of resemblance.
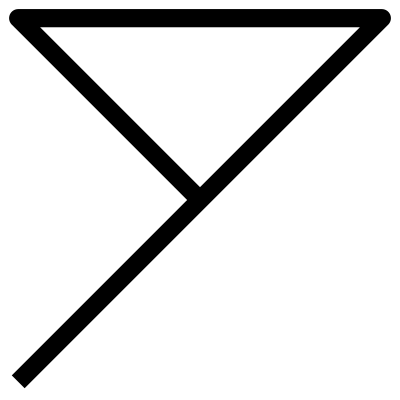
I currently have no other symbols, but expect to later.